| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 컴퓨터 구조
- 멀티스레드
- BFS
- 혼자공부하는
- 스레드
- Transform
- 지역변수
- 코딩테스트
- 풀이
- CPU 스케줄링
- DirectX
- static
- 운영체제
- 컴퓨터구조
- 혼자 공부하는
- dfs
- 인터럽트
- C++
- 독학
- 입출력장치
- 장치컨트롤러
- DDR SDRAM
- 프로세스
- 보조기억장치
- 131701
- 한빛미디어
- 프로그래머스
- 렌더링 파이프라인
- 그래프
- 138477
- Today
- Total
빼미의 개발일기
[DirectX] - 01. 변환 (Transform) (1) 본문
● 변환 (Transform) : 지오메트리를 조작하는 기본 도구.
1) 기본 변환
1.1) 이동 (Translation)
- 이동 행렬 T는 한 위치에서 다른 위치로의 변화를 나타내며, $t = ( t_{x}, t_{y}, t_{z})$로 요소를 변환한다.
$$ T(t) = T( t_{x},t_{y},t_{z}) = \begin{bmatrix}1 & 0 & 0 & t_{x} \\0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} $$
- 예를들어 $T(5,2,0)$ 이동행렬이 있고, $O(x,y,z)$ 를 갖는 정점이 있다고 가정 했을 때
$$ \begin{bmatrix}1 & 0 & 0 & 5 \\0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix}O_{x} \\ O_{y} \\ O_{z} \\ 1 \\ \end{bmatrix} = \begin{bmatrix}O_{x} + 5 \\ O_{y} + 2 \\ O_{z} + 0 \\ 1 \\ \end{bmatrix} $$
- 와 같이 계산 할 수 있다
- 방향 벡터는 이동 할 수 없기 때문에 백터 $v = (v_{x}, v_{y}, v_{z}, 0)$ 는 T에 의한 곱의 영향을 받지 않지만, 아핀변환에선 영향을 받는다
- 이동행렬의 역행렬 $T^{-1}(t) = T(-t)$로, 즉 백터 t가 음이 된다. (증명하기엔 너무 길다)
※ DirectX에선 아래쪽 행에 변환 백터가 있는 행렬을 사용하는데, 행렬의 순서가 역순, 즉 적용 순서가 왼쪽에서 오른쪽으로 읽는 방식이다.
$$ \begin{bmatrix}O_{x} & O_{y} & O_{z} & 1 \\ \end{bmatrix} \begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 5 & 2 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix}O_{x} + 5 \\ O_{y} + 2 \\ O_{z} + 0 \\ 1 \\ \end{bmatrix} $$
- 이런 방식은 백터가 행이기 때문에 행 우선 방식이라고 한다.
1.2) 회전 (Rotation)
- 원점을 통과하는 축을 중심으로 백터를 주어진 각도로 회전 변환 한다.
- 2차원에서 회전 행렬을 도출했을 때, $v = (v_{x}, v_{y}) = (r cos \theta , r sin \theta)$ 라는 벡터가 있다 가정한다.
이 벡터를 $\phi$ 라디안 만큼 회전한다면 $v = (r cos \theta + \phi , r sin \theta + \phi )$ 를 얻게 되는데, 이를 확정하면 다음과 같은 관계를 얻을 수 있다.
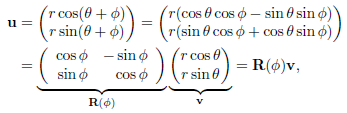
- 일반적으로 사용되는 회전 행렬은 $R_{x}(\phi), R_{y}(\phi), R_{z}(\phi) $ 이며, $\phi$ 라디안 만큼 x, y, z 축으로 각각 회전시킨다.
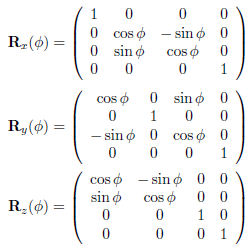
- 여기서 $ R_{y}(\phi) $ 은 $sin \phi $ 의 부호가 서로 바뀐 것에 주목해야 하는데, 이는 자이로스코프 회전 방식을 따른 것이다. 자이로스코프에서 X(Pitch)축과 Z(Roll)축은 시계방향을 회전하여 양수지만, Y(Yaw)축은 반시계방향으로 회전할수록 양수이다.
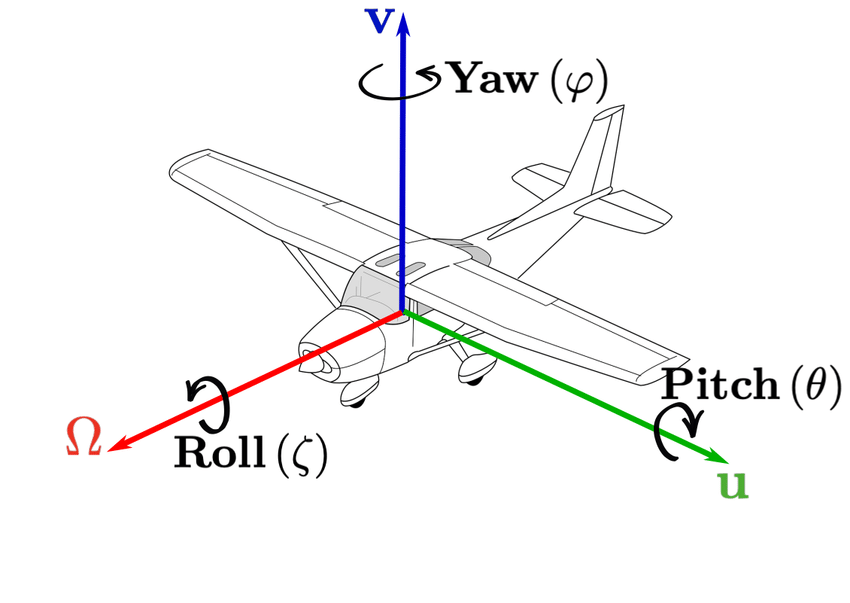
- 모든 회전 행렬은 행렬식(determinant - $det(R)$) 값이 1이며 직교한다.
- 또한 역행렬은 $R_{i}^{-1}(\phi) = R_{i}(-\phi)$ 와 같이 동일 축에 대해 반대 방향으로 회전한다.
※ 임의의 점에 대한 회전
- 오브젝트를 z축에 대해 $\phi$ 라디안 회전하고자 할 때 회전에 중심점이 특정 점 p에 있다고 가정한다.
- 이럴 때 특정 점 p 가 z축의 원점으로 오도록 오브젝트를 이동시키고 z축에 대한 회전을 수행한다. 그 후 다시 원래의 위치로 오브젝트를 이동하면 특정 점 p에 대한 회전 수행이 완료되고 이를 행렬연산으로 하면 다음과 같다.
$$X = T(p)R_{z}(\phi)T(-p)$$

1.3) 크기 조절 (Scaling)
- 크기 조절 행렬 $S(s) = S(s_{x}, s_{y}, s_{z}) $는 x, y, z 방향에 대한 각 성분의 인자로 크기를 조절한다.
- 특정 성분을 1로 설정하면 크기는 변경하지 않는다.
$$ S(s) = \begin{bmatrix}s_{x} & 0 & 0 & 0 \\0 & s_{y} & 0 & 0 \\ 0 & 0 & s_{z} & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$$
- 크기 조절 연산이 $s_{x} = s_{y} = s_{z} $라면 균등(uniform), 그렇지 않다면 비균등(nonuniform)이라고 한다.
- 역행렬은 $S^{-1}(s)$ $ = S(1 / s_{x}, 1 / s_{y}, 1 / s_{z})$ 이다
- 동차 좌표를 사용하는 균등 크기 조절 행렬로 위치 (3,3)의 행렬 성분으로 조절하는 방법이 있다.
- 해당 값은 동차 좌표의 w 성분에 영향을 주며 행렬로 변환되는 점에 대한 모든 좌표의 크기를 조절한다.

- 단, $S^{`}$는 동차화가 항상 이어지며, 동차화에서 나누기 과정이 포함되기 때문에 비효율적이다.
- S의 첫번째나 세번째 성분에 대해 음의 값이 있다면 반사 행렬(reflection matrix)의 형태를 제공하며, 이는 거울 행렬(mirror matrix)라고도 한다.
- 2개의 크기 인자만 -1이면 $\pi$ 라디안 만큼 회전한다. 회전 행렬이 반사 행렬과 연결되면 또다시 반사 행렬이 된다.

※ 특정 방향에 대한 크기 조절
- x, y, z 축에 대한 조절이 아닌 다른 방향으로 크기 조절을 하려면 결합 변환이 필요하다. 크기 조절이 직교하는 오른손 좌표계 백터 $f^{x}, f^{y}, f^{z}$의 축에 대해 처리한다고 가정할 때, 축 변환 행렬 F는 다음과 같다
$$F = \begin{bmatrix}f_{x} & f_{y} & f_{z} & 0 \\0 & 0 & 0 & 1 \end{bmatrix} $$
- 세축에 의해 주어진 좌표계에서 각 축을 표준 축과 일치 시킨 후 표준적인 크기 조절 행렬을 하용하고 다시 원래 위치로 되돌린다.
$$ X = FS_{s}F^{T} $$
1.4) 전단 (Shearing)
- 게임 전체 장면에 효과를 생성하고자 왜곡을 하거나 모델의 모습을 비트는데 사용한다
- $H_{xy}(s), H_{xz}(s), H_{yx}(s), H_{yz}(s), H_{zx}(s), H_{zy}(s)$의 여섯가지 기본 전단 행렬이 있다.
- 첫 첨자는 전단 행렬에 의해 변경될 좌표를 나타내고, 두 번째 첨자는 전단 변환을 수행하는 좌표를 표기한다.
- 예를 들어 $ H_{xz}(s) $의 식은 다음과 같다
$$ H_{xz}(s) = \begin{bmatrix}1 & 0 & s & 0 \\0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}$$
- 위의 행렬을 점 p에 대해 곱하면 새로운 점 $(p_{x} + sp_{z} \ p_{y} \ p_{z})^{T}$ 로 이동한다.
- $H_{ij}(s)$의 역행렬은 반대 방향으로 전단 변환하여 얻을 수 있고, $H^{`}_{ij}(s) = H_{ij}(-s) $ 가 된다

※ 이어서
'프로그래밍 > 게임그래픽' 카테고리의 다른 글
| [DirectX] - 01. 변환(Transform) (3) (1) | 2023.12.26 |
|---|---|
| [DirectX] - 01. 변환(Transform) (2) (1) | 2023.12.21 |
| [DirectX] - 00. 렌더링 파이프라인 개요 (3) (1) | 2023.12.18 |
| [DirectX] - 00. 렌더링 파이프라인 개요 (2) (1) | 2023.11.28 |
| [DirectX] - 00. 렌더링 파이프라인 개요 (1) (2) | 2023.11.25 |




